Definizione, etimologia e campo di indagine

Branca della geometria che studia le proprietà dello spazio che permangono invarianti per il gruppo delle trasformazioni topologiche, ovvero quelle proprietà profonde e astratte che si conservano, a seguito di deformazioni impresse senza lacerazioni o sovrapposizioni a configurazioni immaginate elastiche (trasformazioni biunivoche e bicontinue), nonostante l’alterazione delle proprietà metriche e proiettive (rapporto e birapporto fra distanze e angoli). Configurazioni ottenibili l’una dall’altra per questa via, come il cubo e la sfera, si dicono “omeomorfe” o topologicamente equivalenti, e le trasformazioni stesse “omeomorfismi”. Pur nel rigore delle dimostrazioni, oltre agli aspetti metrici (calcolabili ma non sempre essenziali) contano relazioni più intuitive quali apertura e chiusura, regione e frontiera, prossimità, compattezza, orientamento (imprescindibili), suggerendo dirette analogie qualitative con lo “spazio esistenziale”, tema privilegiato dell’architettura altresì evocato dal termine tópos (luogo) che identifica questa geometria.

Struttura dello spazio topologico

In quanto analysis situs (analisi di posizione), nelle ipotesi più astratte non necessariamente riferita a enti geometrici, la geometria topografica distingue configurazioni e spazi in base all’organizzazione degli elementi evidenziata dagli “omeomorfismi”, così stabilendo le proprietà “invarianti”. In primis la “dimensione”, data l’impossibilità di trasformare punti, linee, superfici e volumi gli uni negli altri per mera deformazione.
L’ordine di “connessione”, dato dal numero di “tagli” necessari a dividere configurazioni e spazi, sicché nelle tre dimensioni una superficie sferica (priva di fori) risulta monoconnessa (divisibile da una linea di taglio), una torica (dotata di un foro) biconnessa (due tagli), una a doppio toro (a due fori) triconnessa (tre tagli) e così via, comunque le si deformi. La “continuità” e la “contiguità”, ovvero la persistenza di legami di reciproca posizione fra gli elementi nella distorsione, come avviene per i reticoli elastici, per superfici elastiche incollate lungo i bordi, per volumi deformabili giuntati lungo le facce. Dimensione, ordine di connessione, continuità, contiguità, identificano quindi proprietà generalissime e tuttavia distintive, identificando le “varietà topologiche”, mentre modelli di spazi topologici possono ottenersi come estensioni di specifiche configurazioni, mutuandone le proprietà. Gli spazi topologici possono riguardarsi come insiemi, strutture, categorie, definendo un ambito di studi non ancora esaurito, specie nel campo complesso e nelle dimensioni alte, laddove è necessario introdurre assiomi specifici. Quanto ai legami con altre branche, si noti che gli enti impropri dello spazio proiettivo costituiscono in campo topologico elementi di connessione e di continuità, mentre ulteriori nessi riguardano gli iperspazi, i campi vettoriali, gli oggetti frattali, e altri campi.

Configurazioni notevoli
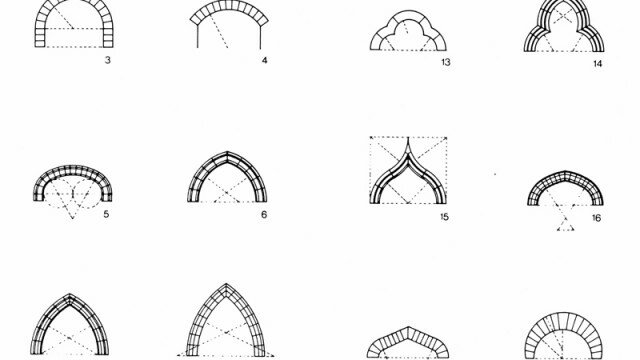
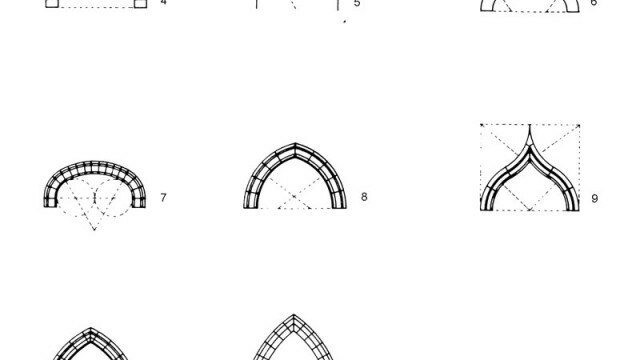
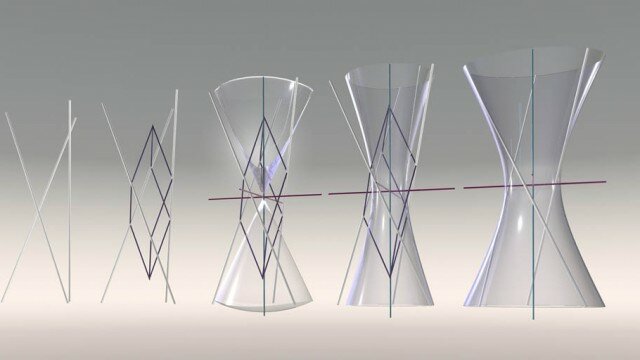
Nastro di Möbius e otre di Klein, calotta intersecantesi, toro tridimensionale, sfera pelosa, nodi, stella baricentrica, ricoprimenti, reticoli, curva di Jordan. In architettura, esemplari la Möbius House (Olanda, 1998) di Ben van Berkel e Caroline Bos (UN-Studio), direttamente ispirata all’omonima superficie, nonché numerose opere conformate sul principio della deformazione (morphing). Nella rappresentazione digitale le superfici poligonali, le NURBS, e in generale i CAD a controllo parametrico riflettono altrettanti aspetti della natura sintetica e analitica di questa geometria.

Cenno storico
Già implicita nelle rappresentazioni figurative della Preistoria, significativa negli studi cognitivi sulle categorie spaziali, la geometria topologica è ufficialmente formalizzata nel 1895 con l’Analysis Situs di Henri Poincaré (1854-1912), a valle della legittimazione delle moderne teorie spaziali con il Programma di Erlangen (1872) di Felix Klein (1849-1925) e appena in anticipo sui nuovi protocolli assiomatici di David Hilbert (1862-1943) in Grundlagen der Geometrie (1899), pur essendo il termine topologia già apparso nel 1847, precisamente nelle Vorstudien zur Topologie di Johann Benedict Listing (1808-1882). Fra i maggiori innovatori, August Ferdinand Möbius (1790-1868) ha il merito di aver definito la superficie a una banda che porta il suo nome, promuovendo lo studio delle superfici di ordine di connessione pari, ovvero topologicamente intermedie tra sfera (monoconnessa) e toro (biconnesso). Si deve, invece, a Felix Klein la superficie a una banda a forma di otre, ottenuta per deformazione e autopenetrazione da una superficie cilindrica, che opportunamente ritagliata dà origine a due nastri di Möbius. Le molteplici e complesse configurazioni ottenibili nel nostro e negli spazi a più dimensioni, hanno evidenziato proprietà fondamentali sia per la matematica che per la fisica contemporanee. Dalle prime deduzioni di Cartesio (1596-1650) e di Eulero (1707-1783) sulla relazione fra numero di spigoli, vertici e facce nei poliedri semplici all’origine della topologia combinatoria o algebrica, alla teoria degli insiemi di Georg Cantor (1845-1918) alla base della topologia insiemistica, le due branche della topologia classica poi affiancate dalla topologia differenziale, altre branche si sono nel tempo sviluppate.
L’origine della moderna geometria topografica si lega, nella sostanza, alle ipotesi non-euclidee di curvatura dello spazio introdotte dalla geometria iperbolica di Nicolaj Ivanovič Lobačevskij (1793-1856) e János Bólyai (1802-1860), e dalla geometria ellittica di Georg Friedrich Bernhard Riemann (1826-1866), e nella formalizzazione algebrica ai decisivi avanzamenti nel calcolo delle superfici curve dovuti a Johann Carl Friedrich Gauss (1777-1855). Soffermandosi sulle proprietà più astratte, la geometria topografica ha in seguito favorito importanti ricerche nel campo dei fondamenti primi della matematica, progressivamente svincolandosi dalla visualizzazione dei risultati. In particolare, nell’ipotesi di Cantor sugli insiemi collegati da funzioni, essa contribuì alla definizione di importanti assiomi e al chiarimento della nozione di classe, nonché all’identificazione di insiemi speciali, fra cui l’insieme infinito e l’insieme inaccessibile, ad opera di Ernst Zermelo (1871-1953), Abraham Fraenkel (1891-1965), Alexandre Grothendieck (1928-), per una fondazione della matematica su basi logiche. Nelle ricerche dei matematici Nicolas Bourbaki (attivi dal 1935 al 1983) sugli insiemi strutturati e le funzioni in grado di conservarne le relazioni, essa contribuì alla messa a fuoco delle nozioni di struttura algebrica, struttura d’ordine, struttura topologica e a esplorarne le combinazioni nell’algebra topologica e nella topologia algebrica, a favore di una fondazione strutturalista della matematica. Nel lavoro di Samuel Eilenberg (1913-1998) e Saunders MacLane (1909-2005) sulla trattazione unificata di insiemi (collegati da funzioni) e strutture (collegate da morfismi) come casi particolari delle categorie (collegate da funtori), sostiene infine l’ambizione di una fondazione globale della matematica in termini categoriali, pervenendo alla teoria dei topoi. In campo informatico maggiori vincoli di concretezza suggerirono un innovativo sistema di calcolo, il Lambda Calcolo, ricordato tra l’altro per il teorema del punto fisso e legato ad Alonzo Church (1903-1995), John Barkley Rosser (1907-1989), Stephen Cole Kleene (1909-1994), i quali definirono le funzioni base della programmazione informatica, precorrendo la semantica denotazionale di Dana Scott (1932), che equiparando i programmi di calcolo a oggetti matematici, legittimò l’informatica come branca matematica.

Bibliografia

Boyer C.B., Storia della Matematica, Mondadori, Milano, 1980; Courant R., Robbins H, Che cos’è la Matematica?, Bollati Boringhieri, Torino, 2000; Hilbert D., Cohn-Vossen S., Geometria Intuitiva, Bollati Boringhieri, Torino, 2001; Odifreddi P., La matematica del Novecento. Dagli insiemi alla complessità, Einaudi, Torino, 2000.

Topologica, geometria cocchiarella-luigi

www.Wikitecnica.com