Categoria

Arco (storia)

Definizione-Etimologia

Dal latino arcus. Il termine indica una struttura portante ad asse curvilineo, i cui estremi poggiano generalmente su piedritti o colonne.

Storia

In modo rudimentale il principio costruttivo dell’arco è rilevabile nella necropoli di Abido (Egitto, circa 2300 a.C.), in una volta costituita da conci (
concio) di pietra alternati con mattoni crudi, tenuti insieme da una malta embrionale, che consentono la convergenza dei conci al centro di curvatura, e in altri esempi dell’area mediorientale; ma le più antiche strutture che applicano il sistema dell’arco a conci radiali sono precedute da altre (pseudoarchi), ottenute sia con uno o due grandi blocchi accostati e scavati a sagoma curvilinea, sia con materiali di taglia modesta, a letti orizzontali progressivamente aggettanti. Queste tecniche continuano a essere usate anche successivamente alle esperienze a conci radiali ricordate, confermando che l’arco non è il risultato dell’intuizione delle sue proprietà statiche, ma più genericamente una forma connessa all’esigenza di coprire una luce rilevante.
L’impiego, nelle coperture, di pseudoarchi e archi parzialmente non spingenti ha anche il fine, in aree povere di legname, di evitare le centine. A questo scopo un’altra tecnica adottata è costituita da una serie di archi a conci disposti su un piano non verticale ma inclinato, appoggiati l’uno sull’altro e infine al muro di fondo dell’ambiente, sul quale si scarica il peso di ogni singolo strato.

In Egitto, come pure in Mesopotamia, dove le prime testimonianze di archi sembrano risalire al VI millennio a.C., questi tipi di coperture ad arco sono utilizzati esclusivamente in ambito funerario o per ambienti secondari, quali cunicoli, corridoi o magazzini.
I greci conobbero, accanto ai vari tipi di pseudoarchi, l’archi a conci, del quale, come riferisce Seneca, sarebbe stato inventore Democrito (V secolo a.C.), ma il cui impiego è documentato, su base archeologica, solo dagli ultimi decenni del IV secolo a.C., nelle tombe a camera macedoni (tomba regale di Verghina, circa 336 a.C.), nelle porte di cinte murarie (Eniade in Acarnania), e in coperture di cisterne, corridoi o disimpegni di teatri, stadi e complessi religiosi. Si riscontra anche l’impiego di archi ciechi affiancati, a sostegno di un pendio o di strutture soprastanti (fortificazioni di Perge in Pamphilia).

Nell’Italia meridionale greca e sannitica l’uso dell’arco a conci viene introdotto in costruzioni tombali a camera agli inizi del III secolo a.C.; è discussa l’attribuzione alla metà del IV secolo a.C. (contemporanea alle più antiche esperienze macedoni) della cosiddetta Porta Rosa di Velia. Certamente del IV secolo a.C. è la volta della tomba di Charun presso Cerveteri, che attesta la precoce introduzione delle strutture ad arco in Etruria, mentre la Porta dell’Arco di Volterra e le porte di Perugia, per le quali è stata proposta una datazione alta, sono oggi ritenute del II secolo a.C. Scarsa, per l’architettura etrusca, la documentazione relativa alle costruzioni civili, ma è integrata da rappresentazioni scolpite o dipinte.
Per l’architettura romana, l’impiego di strutture ad arco è documentato intorno alla metà del III secolo a.C. in porte urbiche (Cosa), ponti e viadotti, ma è nel secolo seguente che le strutture ad arco trovano applicazione generalizzata, estesa alla copertura di ampi ambienti interni (Porticus Aemilia, 193-174 a.C.), grazie alla tecnica dell’opus caementicium, diventando una caratteristica basilare delle maggiori realizzazioni architettoniche romane.
Il trapasso dell’arco da elemento tecnico e utilitario a motivo strutturale monumentale si compie con la sua integrazione al sistema trilitico, negli edifici con facciata costituita da una serie di archi su pilastri, ma inquadrati da semicolonne che sorreggono una trabeazione applicata alla parete. Il motivo, già presente nei santuari laziali della fine del II secolo a.C., e, a Roma, nel Tabularium (78 a.C.), diventa la soluzione ricorrente per definire grandi superfici esterne, anche sviluppate su più piani, e trova applicazione negli archi onorari e negli ingressi monumentali.

In seguito, nel medio e tardo impero, gli archi sono impostati direttamente sulle colonne (Foro e Via Colonnata di Leptis Magna, peristilio del Palazzo di Diocleziano a Spalato), o con l’interposizione di un elemento di architrave (Santa Costanza a Roma). Una soluzione particolare è rappresentata dall’architrave che si interrompe piegandosi in forma di archi (il cosiddetto frontone siriaco, nel tempio di Adriano a Efeso).
I romani hanno usato essenzialmente l’archi semicircolare (a tutto sesto); l’arco ribassato o segmentato, la cui forma è data da un segmento di circonferenza, trova applicazione in casi particolari, come le finestre termali, e negli archi di scarico per i quali è frequente anche la piattabanda.
Le culture architettoniche che di Roma raccolgono l’eredità adottano anche varianti e forme diverse: i bizantini fanno largo uso di archi a tutto sesto su piedritti rialzati, impiegati anche dagli arabi insieme all’arco a ferro di cavallo, specialmente diffuso in Spagna e Africa settentrionale; l’arco ellittico e quello ribassato policentrico sono poco usati nell’architettura tardo-antica e medievale, ma troveranno maggiore successo nel Rinascimento e nel Barocco, in particolare nella costruzione di ponti in muratura.
Gli archi acuti sono costituiti da due tratti di circonferenza, i cui centri sono posti sul piano della corda, a distanza variabile dall’asse, che ne determina la forma più o meno allungata: archi acuti equilateri, se i centri di curvatura coincidono con i punti d’imposta; compressi se interni alla corda; a lancetta se esterni; lanceolati, quando inoltre si trovino sopra il piano d’imposta.

L’impiego degli archi acuti, a parte l’esempio precoce di Qasr-Ibn-Wardan (561-564), è fatto risalire all’architettura islamica del secolo VIII; queste forme si diffondono in Italia e in Europa intorno all’XI secolo, ma l’uso sistematico che ne fanno i costruttori gotici, a partire dagli inizi del XII secolo, è il frutto di osservazioni autonome sui vantaggi pratici nella realizzazione delle volte a crociera e sul contenimento della spinta, offerti da questo tipo di arco, come testimonierebbero le formule pratiche e i tradizionali procedimenti grafici di dimensionamento dei piedritti, noti attraverso la letteratura posteriore, ma probabilmente in uso già in epoca medievale.
Forme particolari sono l’arco falcato (conci di altezza crescente dall’imposta alla chiave), o l’arco senese (con intradosso a tutto sesto ed estradosso acuto). Altri tipi di archi policentrici sono stati impiegati per motivi formali e di gusto: l’arco polilobato, con intradosso costituito da una serie di archetti (lobi) i cui centri di curvatura sono posti ad altezze diverse, indica in genere influenze arabe; l’arco trilobato, presente in una grande varietà di forme, è ampiamente usato, nel tipo con archetto centrale acuto, per finestre, porte e decorazioni del gotico rayonnant; l’arco inflesso (in inglese ogee arch), a quattro centri e profilo concavo-convesso-concavo, di origine orientale e introdotto in Occidente attraverso Venezia, si afferma in Inghilterra con il decorated e si diffonde con il tardogotico, anche nella variante a profilo convesso-concavo-convesso (arco a fiamma, in francese arc en doucine), variante usata soprattutto nei trafori delle finestre. L’arco inflesso si arricchisce poi con l’immissione, tra i principali tratti curvilinei, di altri lobi e segmenti rettilinei, che ne complicano il profilo. Un’ulteriore variante è l’arco Tudor, con archivolto costituito da due archetti concavi raccordati da due tratti rettilinei (o da due tratti di circonferenza con raggio di curvatura molto ampio), uniti a cuspide, tipico dell’architettura inglese dal XV al XVIII secolo.
L’architettura moderna, dopo il periodo storicista ed eclettico, con l’introduzione delle nuove tecniche costruttive e dei nuovi materiali, ha abbandonato nell’architettura corrente l’uso dell’arco, il cui impiego rimane limitato alle grandi strutture (ponti, viadotti ecc.), e ad alcune opere di particolare significato simbolico e monumentale.

Bibliografia

Bettini S., L’architettura di San Marco, Padova, 1946; s.v. Arco, in Enciclopedia dell’arte antica, Secondo Supplemento 1971, Roma, 1994, pp. 344-354.

Photogallery
Categoria

Arco (costruzioni)

Definizione-Etimologia

Dal latino arcus. Il termine indica una struttura portante ad asse curvilineo, i cui estremi poggiano generalmente su piedritti o colonne.

Generalità

A differenza dello schema trilitico, in una struttura ad arco l’elemento orizzontale, arcuato, non è semplicemente inflesso ma è anche compresso e i due piedritti che lo sostengono ricevono non solo carichi verticali ma anche una spinta orizzontale tendente a ribaltarli verso l’esterno. L’arco costituisce un compromesso tra elemento orizzontale e verticale, deviando progressivamente i carichi verticali sui piedritti (o spalle) fino a condurli a terra. Per evitare il possibile ribaltamento dovuto alle spinte orizzontali che sono chiamati ad assorbire, i piedritti devono essere costituiti da abbondanti masse murarie di contrasto, in modo che spinta e peso, composti vettorialmente, si mantengano entro il terzo medio della sezione in muratura.
Creato per funzionare a compressione, l’arco ha rappresentato per secoli la migliore soluzione costruttiva per il materiale muratura e l’evoluzione dei diversi stili architettonici si può vedere come la storia delle soluzioni costruttive per contenere le spinte orizzontali sui piedritti e mantenere le sezioni arcuate puramente compresse.

Parti costitutive delle strutture ad arco

Nella realtà costruttiva, l’arco è costituito da più elementi, detti conci (
concio), che si trasmettono le forze per attrito o contatto reciproco, per interposizione di materiale legante, per introduzione di perni e staffe o per incastro.
Si definisce asse dell’arco il luogo dei baricentri delle sezioni costituenti, e la sua forma, insieme ad altri parametri (corda, freccia e spessore), è un elemento essenziale per definire l’effettiva capacità dell’arco di sopportare i carichi.
L’arco si sviluppa a partire dalla sua base (imposta), che è la superficie d’appoggio sui piedritti, lungo il suo asse, fino alla chiusura in chiave (o serraglio) attraverso un concio (chiave) geometricamente coincidente con il vertice, che viene posto in opera per ultimo garantendone la stabilità (centina, concio).
La struttura ad arco è compresa tra la superficie di intradosso (interna, detta anche imbotto o sottarco) e quella di estradosso (esterna).
La distanza tra i punti estremi delle sue linee d’imposta si dice corda (luce, ampiezza, portata o sottesa), ed è un importante parametro per la stabilità dell’arco, insieme alla freccia (monta o saetta) che ne definisce l’altezza.
Si definisce piano d’imposta dell’arco il piano contenente le sue linee d’imposta o anche la superficie (piana o inclinata) della faccia superiore del concio da cui l’arco si sviluppa (peduccio o pulvino).
Lo spessore di un arco, non necessariamente costante, è definito come la distanza tra intradosso ed estradosso, misurata sull’archivolto; tale misura può variare tra imposta e chiave (ad esempio nell’arco senese).
La superficie ideale compresa tra linea d’intradosso e linea d’imposta viene detta specchio dell’arco e qualora sia cieca o murata si definisce lunetta, mentre si chiama sopraporta o soprafinestra nei casi in cui sia integrata negli infissi che chiudono l’apertura.

Tipologie

Considerando l’andamento della curva d’intradosso in relazione al proprio sesto (o profilo) definito come rapporto tra freccia e metà della luce, gli archi si distinguono in: archi a tutto sesto (pieno sesto o pieno centro, tondi) in cui la freccia è pari a metà della luce e la curva d’intradosso è una semicirconferenza; archi a sesto rialzato (eccedente o oltrepassato), la cui freccia è superiore a metà corda (archi a ferro di cavallo, archi a sesto acuto lanceolati, archi polilobati, archi con curva d’intradosso composita inflessi o carenati); archi a sesto ribassato (scemi, tondi ribassati, a monta depressa, schiacciati o diminuiti), il cui intradosso è un tratto di semicirconferenza con il centro a quota inferiore alle imposte e con freccia inferiore a metà corda (archi rovesci). Gli archi policentrici, composti, asimmetrici, derivano la loro forma dalla posizione dei centri di curvatura che possono essere lungo la linea d’imposta (arco acuto), sopra di essa (arco lanceolato), in bande opposte rispetto all’intradosso (arco inflesso o carenato) o ad altezze diverse (arco polilobato). Per ciascuno di questi archi diversi sono i metodi di tracciamento e di costruzione.
A seconda delle caratteristiche e della posizione delle linee d’imposta gli archi possono essere retti (linee d’imposta normali alle fronti) o obliqui (non perpendicolari alle fronti). Gli archi rampanti hanno linee d’imposta parallele ai fronti ma inclinate rispetto all’orizzontale mentre negli archi zoppi (o a collo d’oca) queste sono parallele tra loro e orizzontali ma a quote diverse. A seconda che abbiano una sola o diverse curvature, tra loro raccordate, gli archi si distinguono in continui e discontinui.

Funzionamento statico dell’arco

La parte di muratura appoggiata all’estradosso, in corrispondenza dei fianchi (o reni) dell’arco, è detta rinfianco e ha funzione di rinforzo. Procedendo verso gli appoggi, generalmente aumenta la sezione resistente dell’arco, in considerazione dell’aumento del carico applicato passando dalla chiave alle reni. La linea delle successive risultanti, detta anche curva delle pressioni, caratterizza ogni arco e la sua determinazione è necessaria per la verifica della sua stabilità. Tale linea visualizza il modo in cui le forze si trasmettono tra i singoli conci e la sua curvatura dipende dalla configurazione dei carichi gravanti sull’arco (pesi propri e sovraccarichi) oltre che dalla geometria dell’arco stesso.
La coincidenza tra asse dell’arco e curva delle pressioni garantisce che le forze scambiate tra i conci costituenti siano semplicemente di compressione in ogni sezione; maggiore è la distanza tra le due curve e più la risultante dei carichi in ogni sezione risulterà inclinata rispetto alla perpendicolare condotta per il piano della sezione stessa, e lontana dal suo baricentro, determinando l’insorgere di un momento flettente.
Per la soluzione statica dell’arco il metodo più usato è quello grafico, che consiste nella costruzione del poligono funicolare del sistema di vettori rappresentanti i pesi dei singoli conci, imponendo il suo passaggio in chiave e alle reni per le cerniere individuate sperimentalmente da Mery (poste tra i 30° e 45° a partire dall’orizzontale, a seconda della geometria).
Analiticamente, la struttura, iperstatica, si risolve determinandone le reazioni vincolari sui piedritti, imponendo l’equilibrio esterno, e quindi esaminando le sollecitazioni sulle singole sezioni (momento flettente, sforzo di taglio e sforzo normale) dopo aver introdotto alcune ipotesi semplificative che fanno capo alla simmetria della struttura e alla posizione delle cerniere (arco a tre cerniere, staticamente determinato, la cui soluzione viene definita attraverso il tracciamento di un poligono funicolare che connette i carichi applicati e passa per tre cerniere). Il comportamento dell’arco tradizionale (compresso, in muratura) deve essere distinto da quello costituito da una fune flessibile alla quale sono applicati i carichi (teso, come nel caso della catenaria o dei cavi nei ponti sospesi) la cui soluzione statica è relativamente recente (i maggiori sviluppi sono dovuti agli studi di L.F. Menabrea e di A. Castigliano).

Bibliografia

Photogallery

Benvenuto E., La scienza delle costruzioni nel suo sviluppo storico, Firenze, 1981; Choisy F.A., L’art de bâtir chez les romains, Parigi, 1873; Giuffré A., La meccanica nell’architettura, Roma, 1986.
Categoria

Espressionismo

Definizione – Etimologia

Con il termine espressionismo si usa definire il movimento architettonico sviluppatosi in Europa nei primi decenni del ventesimo secolo in seguito all’analogo movimento della arti visive e dello spettacolo rivolte a privilegiare, esasperandolo, il dato emotivo della realtà rispetto a quello percepibile oggettivamente. Tale tendenza si è manifestata in molte forme d’arte, come la pittura, la danza, la letteratura, l’architettura, il cinema, il teatro, la musica.

Generalità

L’espressionismo è una tendenza dell’avanguardia artistica sviluppatasi tra il 1905 e il 1925 in Germania; proponeva una rivoluzione del linguaggio che contrapponeva all’oggettività dell’impressionismo la soggettività dell’espressionismo. L’impressionismo rappresentava una sorta di moto dall’esterno all’interno, cioè era la realtà oggettiva a imprimersi nella coscienza soggettiva dell’artista; l’espressionismo costituisce il moto inverso, dall’interno all’esterno: dall’anima dell’artista direttamente nella realtà Einfühlung, senza mediazioni e con un forte impegno sociale. Organo ufficiale dell’espressionismo fu la rivista «Der Sturm», fondata e diretta da Herwarth Walden e pubblicata dal 1910 al 1932.

Derivazione, processo formativo e filoni tipologici

L’Art Nouveau e le architetture di Antoni Gaudì e di Henry Van de Velde (in particolare il teatro del Werkbund a Colonia del 1914) possono considerarsi precedenti, insieme con le opere della scuola di Amsterdam – ad es. i quartieri di De Klerk e lo Scheepvarthuis di van der Meij 1911-13 nella stessa città – nonché con la goticizzante chiesa Grundtvig a Copenaghen (1913-26) di Peder Klint.

Max Berg con la Jahrhunterthalle di Bleslavia (Wroklaw) 1910-13 può considerarsi espressionista perché travalica la funzione per esprimere forti suggestioni simboliche. Nel 1914 Bruno Taut con Walter Gropius, e il poeta Paul Scheerbart fonda il gruppo Die gläserne Kette (la catena di vetro) e costruisce il padiglione di vetro all’esposizione del Werkbund di Colonia, prototipo di una nuova architettura per un uomo nuovo; durante la guerra schizza utopiche architetture di cristallo lucenti in cima alle vette che pubblica in Alpine Architektur, 1918 e Die Stadtkrone, 1919. Nel 1918 Taut diviene direttore dello Arbeitsrat für Kunst e fonda la rivista «Frühlicht». Nel 1919 organizza con Walter Gropius e con Hermann Finsterlin, autore delle fantastiche forme disegnate esposte nella mostra degli architetti sconosciuti (Ausstellung für unbekannte Architekten).

Dal 1921 al 1924 è impegnato come Stadtbaurat a Magdeburgo progettando alloggi popolari oltre a intraprendere iniziative quali la “Magdeburgo colorata”, operazione di rinnovamento urbano che usava la coloritura delle facciate su teorie psicologico-simboliche (Goethe, Steiner, Itten) affidandole ad artisti. Nella Germania economicamente e moralmente distrutta dalla sconfitta del 1918 il Novembergruppe unisce architetti, pittori, letterati e musicisti, ma pochi poterono costruire i loro progetti. Fanno eccezione: Hans Poelzig (Grosses Schauspielhaus a Berlino 1919, distrutta, scenografie per il film Der Golem, progetti per Max Reinhardt e per la sede del Festival di Salisburgo, non realizzata), Erich Mendelsohn (torre Einstein a Potsdam 1920-21, fabbrica di cappelli a Luckenwalde 1921-23) e Hans Scharoun che inizia la sua attività a Breslavia (Wroklaw) .

Nel 1920-21 Gropius e Hannes Meyer costruiscono casa Sommerfeld a Berlino in blockbau di legno e a Weimar il Monumento ai Caduti di Marzo. Mies van de Rohe in studio con Hugo Häring progetta grattacieli di vetro 1919-21 e poi il monumento a Karl Liebknecht e Rosa Luxemburg 1926 in mattoni a vista distrutto dai nazisti, mentre Häring costruisce la fattoria Gut Garkau 1923-25. Insieme creano nel 1923 in gruppo Zehnerring (anello dei dieci) con Otto Bartning, Peter Behrens, Mendelson, Poelzig, Walter Schilbach, Ludwig Hilberseimer, Bruno e Max Taut.

Amburgo e Brema ebbero un loro espressionismo con la Chile Haus di Fritz Höger 1922-23 e la Haus Atlantis di Bernhardt Hötger 1931, costruzioni in clinker secondo la tradizione anseatica.

Il secondo Goetheanum di Rudolf Steiner a Dornach (Svizzera) del 1923 tutto in cemento armato è un influente esempio di architettura espressionista.

In Italia gli ultimi disegni di Antonio Sant’Elia possono definirsi espressionisti negli scorci di monumentali cattedrali alpine e alla fine degli anni venti Luciano Baldessari è influenzato sia dal futurismo che dall’espressionismo tedesco.

In USA Hugh Ferris illustra la New York City zooning ordinance del 1916 con effetti espressionistici di grattacieli drammaticamente illuminati che ispirano il film Metropolis di Fritz Lang 1927. Dal 1925 Taut, Mendelsohn, Gropius, van de Rohe e Poelzig, insieme con altri artisti espressionisti si rivolsero alla Neue Sachlichkeit (nuova oggettività), un movimento più concreto e pratico, abbandonando le emozioni e i sogni dell’espressionismo.
Molti schizzi e progetti come quelli naturalistici di Finsterlin o dei fratelli Wassilli e Hans Luckardt non si tradussero in edifici, ma Taut nel quartiere Berlin-Britz 1925-31 a ferro di cavallo, Häring, Scharoun, Forbat, Henning, Bartning con Gropius a Siemensstadt 1929-31, Mendelsohn nei suoi grandi magazzini a Berlino, Stoccarda, Breslavia, Chemnitz, Behrens nei quartieri generali della Hoechst AG a Francoforte 1921-25 tutta in mattoni a vista, costruirono una cospicua percentuale dell’architettura moderna degli anni venti in alternativa al razionalismo ortogonale del Bauhaus, trascurata dai disegni storici più diffusi fino alla fine degli anni sessanta.

Accezione moderna del termine

Nel secondo dopoguerra l’opera di Scharoun, la torre Stuttgart (1954), il ginnasio Geschwister-Scholl (1962) e la famosa sala concerti di Berlino (1956-1963), “l’architettura organica” di Häring hanno indicato un’alternativa all’international style influenzando fortemente architetti contemporanei come Le Corbusier, Eero Saarinen, Luis Barragàn (neo espressionismo) e anche in Italia ad esempio Carlo Mollino e a Firenze Giovanni Michelucci, Leonardo Ricci, Leonardo Savioli e Marco Dezzi Bardeschi. Oggi il decostruttivismo di Zaha Hadid, Coop Himmelblau, Daniel Libeskind, Frank O. Gehry, Santiago Calatrava, Enric Miralles e Benedetta Tagliabue ecc attinge dalle utopie tedesche e sovietiche degli anni venti le forme più audaci e barocche realizzate grazie allo sviluppo tecnologico ma depurate da ogni significato sociale.

Bibliografia

Borsi F., König G.K., Architettura dell’Espressionismo, Vitale & Ghianda, Genova, Vincent Freal & Cie, Paris 1967; Pehnt W., Expressionist Architecture, Thames and Hudson, London-New York 1973; Platz G., Die Baukunst der neuesten Zeit, Propylaen Verlag Berlin 1927; Taut B., Die neue Wohnung. Die Frau als Schoepferin, Lipsia, 1924 (tr. it. La nuova abitazione: la donna come creatrice, con introduzione di Paolo Portoghesi, Roma 1986); Taut B., Die Stadtkrone, 1919 (tr. it. La corona della città, con saggio introduttivo di Ludovico Quaroni, Milano 1973; Taut B., Alpine Architektur, Hagen, 1918 (tr. it. La via all’architettura alpina – La dissoluzione delle città – La terra una buona abitazione, Faenza 1976); Zevi B. (a cura), Erich Mendelsohn: opera completa: architettura e immagini architettoniche, Testo & immagine, Torino 1997.

Photogallery

Categoria

Geometria descrittiva

Definizione – Etimologia

La geometria descrittiva è la scienza che studia il modo di rappresentare visivamente le forme a tre dimensioni e studia altresì le loro proprietà geometriche per mezzo di tale rappresentazione. L’espressione geometria descrittiva allude da un lato alla possibilità di misurare le forme suddette (geometria, dal greco γεωμετρία, atto del misurare la terra), dall’altro alla necessità di descriverle per mezzo di immagini (descrittiva, dal latino descríbĕre, descrivere).

Storia

Il termine Géométrie Descriptive fu coniato da Gaspard Monge, alla fine del 1794, per designare un insieme di teorie e procedure grafiche in uso presso il genio militare, da lui codificate nel quadro di una nuova scienza. Queste procedure consistevano, essenzialmente, nell’associare due proiezioni parallele dell’oggetto da rappresentare (la pianta e l’alzato) assumendo i due disegni come piani di riferimento e considerando le intersezioni di rette e piani dello spazio tridimensionale (detti tracce) con i suddetti piani. Così facendo, rappresentazioni tecniche note da secoli potevano proporsi come efficace strumento per la soluzione di problemi progettuali complessi.
Esempi di questi problemi, tipici delle strategie militari dell’epoca, sono il defilamento, ovvero la protezione delle piazzeforti dai tiri dell’artiglieria, o, ancora, la determinazione della posizione nello spazio di un pallone frenato, noti i tre angoli formati dai raggi di collimazione, da uno strumento posto sul pallone, di tre punti noti a terra (problema del vertice di piramide).
Il metodo di Monge si prestava anche alla rappresentazione delle superfici di secondo grado e perciò allo studio sintetico, cioè grafico e non simbolico, delle loro proprietà, nonché alla soluzione di altri problemi squisitamente geometrici come quelli di posizione.
Alla questione del contributo di Monge alla scienza che da lui ha avuto il nome, si danno risposte contrastanti: secondo alcuni egli sarebbe il creatore della geometria descrittiva, secondo altri egli avrebbe solo autorevolmente contribuito a una Storia che ha origini nell’antichità e prosegue ancora ai giorni d’oggi. Ad esempio, le costruzioni grafiche utilizzate da Piero della Francesca nel suo trattato De prospectiva pingendi (scritto tra il 1482 e il 1492), sono a tutti gli effetti proiezioni ortogonali associate come quelle di Monge e, risalendo anche più indietro nel tempo, anche la icnografia e la ortografia vitruviane (I sec.) sono disegni di questo tipo. Inoltre, se si considerano i più recenti strumenti digitali della progettazione architettonica, è possibile ritrovare negli algoritmi e nelle procedure impiegate, ancora teorie e metodi che appartengono in tutto alla geometria descrittiva, perché sono una generalizzazione delle teorie e dei metodi storicizzati.

Ruolo della geometria descrittiva nella scienza e nella tecnica

La geometria descrittiva, già nel tempo della sua prima codificazione teorica, svolge un duplice ruolo: da un lato rappresenta un importante perfezionamento degli strumenti grafici impiegati nel progetto di architettura e di ingegneria, dall’altro integra, con l’immagine e con le logiche tipiche della geometria sintetica, i linguaggi simbolici della geometria analitica e differenziale. A questi due ruoli corrispondono, nell’ottocento, due linee di sviluppo: la prima prevalentemente applicativa, la seconda prevalentemente teorica. Tipici sviluppi applicativi sono quelli che riguardano le arti, tra le quali anche l’architettura, come il disegno degli ordini e la resa del chiaroscuro. I più importanti sviluppi teorici sono invece quelli che riguardano le proprietà delle superfici rigate e delle rigate sviluppabili e la geometria proiettiva.

Struttura della disciplina prima della rivoluzione informatica

La disciplina si è così evoluta fino alla prima metà del Novecento, quando ha consolidato i suoi contenuti in un sistema articolato in tre parti: i metodi, lo studio delle figure geometriche dello spazio, le applicazioni.
I metodi che costituiscono il corpus disciplinare alla metà del novecento sono: la doppia proiezione ortogonale o metodo di Monge, l’assonometria, la proiezione quotata, la proiezione centrale. Lo studio delle superfici riguarda, essenzialmente, i poliedri e le superfici di secondo grado, con qualche accenno a superfici algebriche di ordine superiore al secondo, come il toro e le ciclidi. La terza parte riguarda le applicazioni, che spaziano dalla prospettiva, intesa come immagine e non come metodo autonomo, alla resa degli effetti della luce sui corpi, alla costruzione delle volte, alla stereotomia della pietra e del legno, al progetto degli ingranaggi.
Si perviene così a definire la distinzione tra metodo di rappresentazione e strumento applicativo, che è di fondamentale importanza nell’assetto attuale della disciplina. Ha dignità di metodo quell’insieme di teorie e di procedimenti che consente di rappresentare un oggetto tridimensionale, di operare su di esso come si farebbe sopra un modello fisico e di ricostruire l’oggetto rappresentato nello spazio. Il metodo è tale quando è capace di tutto ciò in completa autonomia e senza l’intervento di altri metodi. Strumento è invece quel sistema che, grazie alla applicazione di uno o più metodi, porta al conseguimento di un risultato efficace nell’ambito dell’attività progettuale o esecutiva. Questa distinzione è fondamentale perché permette, come vedremo, di distinguere due nuovi metodi della geometria descrittiva, dalle applicazioni che ne fanno uso, che sono gli attuali programmi informatici per la modellazione digitale a tre dimensioni.

Modus operandi della geometria descrittiva

Per comprendere appieno il significato della geometria descrittiva nell’ambito del progetto di architettura, occorre ora descrivere il suo modus operandi. Così come nella geometria euclidea il ragionamento astratto, che rispetta le regole del sistema logico-deduttivo, trova nel disegno delle figure piane una verifica sperimentale e la costruzione grafica, a sua volta, dimostra di per sé l’esistenza delle figure; così, nella geometria descrittiva, la ragione che costruisce forme nello spazio trova, nella rappresentazione, la verifica della loro esistenza e, al tempo stesso, le sperimenta, subendo la suggestione di nuove idee. In modo assai semplice e chiaro lo stesso Monge descrive questo effetto euristico, quando descrive i due scopi primari della disciplina: “il primo è rappresentare con esattezza, su un disegno che ha due dimensioni, gli oggetti che ne hanno tre, e che sono suscettibili di una definizione rigorosa […] il secondo … è dedurre, dalla descrizione esatta dei corpi, tutto ciò che segue necessariamente dalle loro forme e posizioni reciproche. In questo senso, è un mezzo di ricerca della verità; essa offre continui esempi del passaggio dal noto all’ignoto”.
Dunque, mentre per un verso il disegno svela l’immagine di forme solo intuite nella mente del progettista, per l’altro, proprio perché rimuove quel velo, mostra proprietà ignote e problemi inaspettati. Tale è anche, e senza alcuna distinzione, il carattere della ricerca scientifica pura, quando la semplice visualizzazione di una figura ideata in astratto, come il prodotto di movimenti e intersezioni, suggerisce risultati che si era ben lungi dall’immaginare. E non è un caso se il verbo costruire ha il medesimo uso nell’ambito della geometria astratta e nell’ambito del cantiere; al punto che la geometria descrittiva si può intendere, semplicemente, come un esercizio astratto dell’arte di progettare.
Le operazioni che il progettista esegue per mezzo della geometria descrittiva appartengono a tre tipi: la visualizzazione delle forme che ha immaginato, la misura delle stesse e la loro costruzione. Queste tre attività non si susseguono in un ordine prestabilito ma si alternano in un processo iterativo, che converge verso la definizione compiuta dell’idea progettuale.
Per quasi tutto il Novecento, gli strumenti grafici impiegati nello svolgimento delle suddette operazioni sono stati la riga e il compasso (come per la geometria classica) e, al più, alcuni ausili tecnici come il tecnigrafo. Nei primi anni Ottanta, con la diffusione dei primi personal computer, e dei primi plotter, l’accuratezza del disegno di progetto è decisamente migliorata, ma la geometria descrittiva ha continuato a svolgere i ruoli che la storia le aveva assegnato. Alla fine degli anni Ottanta, però, sono comparsi i primi elaboratori elettronici personali capaci di prestazioni tridimensionali e, da qualche anno ormai, queste prestazioni hanno raggiunto una perfezione prima inimmaginabile, tale che oggi è possibile costruire una forma a tre dimensioni modellandola in uno spazio virtuale interattivo e ricavare da questa forma i relativi disegni tecnici (piante, alzati, sezioni etc.) in modo automatico.

Struttura della disciplina dopo la rivoluzione informatica

Bisogna, dunque, prendere atto del fatto che la geometria descrittiva ha subito una trasformazione epocale: il primo dei suoi compiti storici, la visualizzazione, è oggi assolto egregiamente dalle macchine; resta invece, con tutta la sua rilevanza, il secondo degli scopi: quello che è connesso con la parte più creativa dell’attività progettuale, e cioè la costruzione delle forme ideate e la verifica che disvela i caratteri nascosti, ignoti, dell’idea.
Nello svolgimento di questo secondo compito, la geometria descrittiva è oggi assistita dalle macchine digitali molto meglio di quanto non sia stata assistita, in passato, dalla riga e dal compasso. Infatti: l’accuratezza del disegno tecnico è passata dal decimo al millesimo di millimetro; la suddetta accuratezza è ulteriormente incrementata dal fatto di poter disporre gli enti geometrici rappresentati direttamente nello spazio, senza la mediazione delle proiezioni; la costruzione si avvale non solo della retta e del cerchio, ma di qualsiasi altra linea, dato che l’accuratezza del tracciamento è la medesima; la costruzione si avvale non solo delle linee piane ma, nello spazio, anche delle superfici.
Le macchine digitali hanno anche esteso il carattere della ripetibilità. Mentre all’epoca di Monge si potevano considerare ripetibili, e perciò rappresentabili nel senso proprio del termine, solo le forme ‘suscettibili di una definizione rigorosa’, oggi sono ripetibili anche forme libere, come sono, ad esempio, le carrozzerie delle automobili, gli scafi e le complesse superfici curve dell’architettura contemporanea. Ciò si deve alla matematica delle equazioni
NURBS (Non Uniform Rational B-spline), capace di rappresentare con esattezza quelle forme libere, irrazionali, che un tempo erano classificate come linee e superfici grafiche.
Infine, la sinergia tra la geometria della rappresentazione visiva e la geometria simbolica, consente oggi l’uso di strumenti che erano prima estranei al mondo della progettazione. Un esempio tra tutti è l’impiego del chiaroscuro (e delle linee isòfote, in particolare) nel controllo della continuità tra superfici. Questa applicazione è comune nella progettazione di componenti stampate dall’aspetto lucido, come quelle di plastica, vetro o metallo.
Alla luce di questi avvenimenti e delle considerazioni che ne sono scaturite, è stato recentemente proposto un nuovo assetto della geometria descrittiva, intesa come scienza che fornisce il fondamento teorico e gli strumenti operativi al disegno di progetto in tutte le sue declinazioni, siano esse grafiche tradizionali o digitali e innovative.
Ai metodi di rappresentazione classici, che restano il presidio del disegno manuale, si sono aggiunti i due metodi della rappresentazione matematica e della rappresentazione numerica o poligonale, che si trovano applicati nei principali programmi per il CAD (Computer Aided Design).
Il primo di questi metodi descrive le forme per mezzo di equazioni e può limitarsi alla rappresentazione delle superfici o estendersi alla rappresentazioni dei volumi, distinguendo il pieno dal vuoto (modellazione solida). Il secondo descrive invece le forme per mezzo di liste, che raccolgono le coordinate dei vertici di un poliedro, che approssima le forme stesse, e altre semplici informazioni, che riguardano la connessione dei suddetti vertici per mezzo di spigoli e facce. La differenza tra questi due metodi è la stessa che, nella geometria descrittiva classica, distingue il tracciamento continuo di una figura, dalla costruzione per punti della medesima e cioè: nella rappresentazione matematica la descrizione delle linee e delle superfici è continua, esatta in ogni punto, mentre nella rappresentazione numerica o poligonale la descrizione delle linee e delle superfici è discreta, esatta solo in alcuni punti caratteristici. Perciò, il primo metodo si presta alle costruzioni canoniche della geometria, come le intersezioni; mentre il secondo metodo si presta a costruzioni meno accurate ma più agili, come è ad esempio, la resa del chiaroscuro. In analogia a quanto accade con i metodi classici, anche i nuovi metodi hanno impieghi diversi nel progetto di architettura, secondo la vocazione di ciascuno di essi. La rappresentazione matematica, come la rappresentazione in pianta e alzato, è atta a esercitare un completo e accurato controllo metrico della forma, mentre la rappresentazione numerica, come la prospettiva, è adatta a esercitare il controllo percettivo dello spazio progettato.
Il riassetto della disciplina comprende poi l’adozione di nuovi strumenti per l’indagine e la costruzione geometrica; questi strumenti derivano dalla possibilità di utilizzare il calcolo digitale agendo, però, sui suoi effetti sintetici, cioè direttamente sulla forma. Ciò significa, ad esempio, utilizzare nella costruzione geometrica le coniche e le quadriche, e non solo la retta e il cerchio, ma anche punti notevoli come il baricentro (non solo delle figure piane, ma dei solidi) avendo così accesso a soluzioni generali che, in passato, erano confinate nel campo delle speculazioni teoriche. In questo senso, la nuova geometria descrittiva non fa che realizzare un auspicio dello stesso Monge, quando immaginava le potenzialità di una scienza capace di unire l’esattezza dell’analisi alla immediatezza visiva della geometria di sintesi.

Bibliografia

Fasolo O., Fondamenti geometrici della rappresentazione progettuale e tecnica dell’architettura, Roma 1980; Migliari R., Geometria descrittiva, Torino, 2009; Migliari R., Geometria dei modelli, Roma, 2003;
Saccardi U., Elementi di Proiettiva – Applicazioni della Geometria Descrittiva, Firenze 2004.

Photogallery
Categoria

Accessibilità (tecnologia)

Definizione ed evoluzione del termine

In senso generale, l’accessibilità esprime la capacità di un ambiente di garantire ad ogni persona, a prescindere dall’età, dal genere, dal retroterra culturale e dalle abilità fisiche, sensoriali e cognitive, una vita indipendente.
Attiene all’esercizio di diritti inviolabili della persona, quali le libertà di movimento e di autodeterminazione, ed è un indicatore privilegiato del livello di permeabilità e di inclusione sociale di una comunità.
In architettura, per accessibilità si intende “l’attitudine di luoghi, prodotti e servizi a essere identificabili, raggiungibili, comprensibili e fruibili autonomamente, in condizioni di comfort e di sicurezza, da parte di chiunque.”
La tematica, che riguarda il complesso degli interventi di trasformazione dell’habitat, è regolata nel nostro Paese da un corpo piuttosto consistente di norme tecniche (in particolare: D.M.LL.PP. 236/1989, relativo all’edilizia privata e residenziale pubblica sovvenzionata ed agevolata; D.P.R. 503/1996, relativo a edifici, spazi e servizi pubblici).
Il termine ha subíto nel tempo una profonda revisione per effetto, innanzitutto, dell’evoluzione del concetto di disabilità, cui è strettamente legato.
Se nel passato la disabilità era, infatti, considerata una condizione della persona, oggi è assunta come il risultato di una complessa interazione tra “persone con menomazioni e barriere comportamentali e ambientali, che impediscono la loro piena ed effettiva partecipazione alla società su base di eguaglianza con gli altri” (Convenzione ONU sui Diritti delle persone disabili, 2006).
Inoltre, se in origine l’accessibilità era associata essenzialmente al soddisfacimento delle esigenze di mobilità delle persone su sedia a ruote, col tempo ha esteso il proprio campo di interesse anche alle esigenze percettive delle persone con minorazioni sensoriali o cognitive (comunicatività ambientale) fino ad essere riferita, oggi, alla generalità delle persone.
Tale apertura d’orizzonte ha condotto, gradualmente, al superamento dell’approccio progettuale basato sulle “soluzioni speciali”, cioè sulla realizzazione di ambienti ad accessibilità riservata e di attrezzature dedicate destinate a questo o a quel profilo d’utenza disabile e all’affermazione di specifiche metodologie progettuali (Design for All, Universal Design, Inclusive Design ecc.) che, con varietà di accenti, mirano a conseguire l’idoneità nell’uso di luoghi, prodotti e servizi per il più ampio spettro possibile di popolazione.
Parallelamente si è diffusa la consapevolezza che l’accessibilità non può essere più intesa riduttivamente come disciplina tecnico-normativa finalizzata all’eliminazione delle barriere architettoniche ma, prima di tutto, come grande valore collettivo, che informa, trasversalmente, tutte le politiche delle Amministrazioni pubbliche (strategia di mainstreaming), che esige la cooperazione tra tutti coloro che intervengono nei processi di trasformazione degli habitat (politici, personale delle amministrazioni pubbliche, progettisti, costruttori, abitanti ecc.) e che necessita di politiche spazio-temporali coerenti alle diverse scale (da quella di dettaglio a quella territoriale) e guidate da adeguati strumenti di programmazione degli interventi, come peraltro previsto dalla normativa vigente (L. 41/1986 e L. 104/1992).
D’altra parte, la letteratura scientifica evidenzia e l’esperienza comune conferma che habitat formalmente ‘a norma’, privi, cioè, delle barriere architettoniche contemplate dalla normativa, non sempre raggiungono un livello di accessibilità soddisfacente.
Il divario tra accessibilità legale e accessibilità effettiva dipende dal fatto che, in un ambiente dato, l’assenza di barriere architettoniche è condizione necessaria ma, di solito, non sufficiente per conseguire l’accessibilità. L’accessibilità, infatti, non si ottiene solo mediante l’eliminazione delle barriere architettoniche (o, nei nuovi interventi, nella loro assenza), ma grazie ad un progetto accurato che trae origine dal quadro delle esigenze da soddisfare. La progettazione accessibile, in pratica, non dovrà porsi solo come adeguamento normativo ma, piuttosto, come strategia di qualificazione ambientale. Ad esempio, un parco urbano per dirsi “accessibile” non solo deve essere privo di barriere architettoniche, ma deve prevedere sedute comode anche per le persone anziane, zone d’ombra, servizi igienici per bambini e per adulti, giochi idonei per tutti i bambini, elettroscooter per le persone che si muovono con difficoltà, colonnine SOS per i casi di emergenza ecc.

Gradi di accessibilità e strategie di intervento

Circa il giudizio di accessibilità di luoghi, prodotti e servizi occorre convenire che esso, in termini rigorosi, non potrà essere definito in senso assoluto ma solo come sintesi dei livelli di soddisfacimento (gradi di accessibilità) correlati ai diversi profili d’utenza considerati. Questo perché ogni profilo d’utenza ha specifiche esigenze e non è raro che uno scenario accessibile per un profilo d’utenza non lo sia, o lo sia solo parzialmente, per un altro. Tale sintesi, d’altra parte, sarà transitoria ed incerta per effetto delle continue trasformazioni che interessano gli habitat umani e per la costante evoluzione che riguarda la disciplina.

Analogamente, nei progetti di riqualificazione è difficile che si consegua la piena accessibilità per tutti, ma, più che altro, un innalzamento dei gradi di accessibilità i quali potranno essere valutati mediante l’analisi ponderata di una serie di fattori assunti come riferimento quali la qualità del progetto, la raggiungibilità del manufatto, le risorse economiche disponibili, la qualità gestionale, la capacità di carico del manufatto (ovvero la sua attitudine di sostenere, senza snaturarsi, gli interventi di necessari) ecc.

Le strategie di intervento per conseguire l’accessibilità ambientale possono distinguersi in materiali ed immateriali.
Le prime attengono ad interventi sulla fisicità dell’ambiente e si esprimono, nella forma più avanzata, mediante progetti sapienti capaci di armonizzare, dal punto di vista funzionale, estetico e simbolico, le diverse esigenze, da acquisire, preferibilmente, mediante il coinvolgimento diretto dei portatori d’interessi.
Talvolta la soluzione tecnica specialistica viene celata o elaborata creativamente in modo da ‘allontanarla’ semanticamente dalle ragioni che l’hanno motivata – il superamento delle barriere architettoniche – e dagli utenti che dovrebbero trarne particolare beneficio – le persone disabili – (approccio mimetico).
In altre circostanze, il sistema di vincoli posto dal contesto di intervento o specifiche motivazioni conducono il progettista a ricorrere ad ‘addizioni’ – permanenti o transitorie – che integrano il manufatto di parti e/o dispositivi per soddisfare specifiche esigenze (approccio protesico).
In tutti i casi è indispensabile che il progetto sia ispirato dalla cultura dell’accessibilità sin dalle fasi istruttorie per scongiurare interventi posticci o disorganici.
A livello urbano e territoriale un ruolo essenziale per risolvere i problemi della raggiungibilità di alcuni siti (si pensi ai numerosissimi centri collinari e montuosi del nostro Paese) o della mobilità nelle aree di grandi dimensioni (aeroporti, aree fieristiche, parchi urbani, centri storici, ecc.) (barriere urbanistiche) è svolto dal sistema integrato dei trasporti.
Le strategie d’intervento ‘immateriali’ sono basate sull’informazione (es. guide all’uso delle città consultabili via web), e sono finalizzati ad evitare la mobilità non necessaria e a consentire ad ogni persona, in base alle proprie capacità, di scegliere tempi e modalità dell’interazione ambientale.

Bibliografia

Laurìa A. (a cura), I Piani per l’Accessibilità. Una sfida per promuovere l’autonomia dei cittadini e valorizzare i luoghi dell’abitare, Roma, 2012; Laurìa A. (a cura), Persone “reali” e progettazione dell’ambiente costruito L’accessibilità come risorsa per la qualità ambientale, Rimini, 2003; UNITED NATIONS, Convention on the Right of Persons with Disabilities, 2006.

Photogallery

Home / Lemmi / Costruzioni

Poligono funicolare

Coïsson Eva aprile 11, 2011

Definizione

Il poligono funicolare è una costruzione grafica che consente di rappresentare le successive risultanti di un sistema di forze complanari. Può essere utilizzato per determinare la posizione del la retta d’azione della risultante di un sistema piano di un numero finito di forze, ovvero per individuarne l’asse a momento nullo. Se il numero di forze diventa infinito (quando, cioè, si considerano carichi uniformemente distribuiti), il poligono funicolare diventa una curva funicolare dei carichi.

Generalità

Il poligono funicolare è uno degli strumenti fondamentali della statica grafica, ovvero di quell’insieme di procedure grafiche che permettono la soluzione dei problemi dell’equilibrio mediante la composizione e scomposizione delle forze, rappresentate in maniera convenzionale ed in scala come vettori orientati. L’iniziatore della statica grafica può essere considerato Stevino, con le applicazioni descritte nei suoi Hypomnemata mathematica del 1608, ma il periodo di maggiore diffusione di questi metodi per lo studio dell’equilibrio di sistemi di carichi fu il XIX secolo.

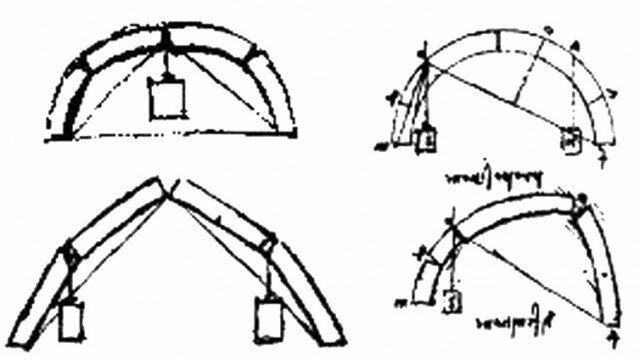
Tracciamento del poligono funicolare (sin.), mediante il poligono delle forze (des.), con individuazione della retta di applicazione della risultante.

Come esempio è rappresentato il procedimento per la costruzione del poligono funicolare di un sistema di 4 forze: si costruisce il poligono delle forze riportando nell’ordine la successione dei vettori che le rappresentano; scelto un polo P, si proiettano da esso i vertici della spezzata così creata e si riportano tali raggi di proiezione parallelamente sul sistema di forze: la spezzata così ottenuta è il poligono funicolare, che rappresenta una delle infinite alla terza configurazioni di equilibrio di una fune sottoposta alle forze agenti. L’intersezione tra le rette del primo e dell’ultimo segmento è un punto della retta d’azione della risultante.

Bibliografia

Benvenuto E., La scienza delle costruzioni e il suo sviluppo storico, Sansoni Editore, Firenze, 1981; Iori I., Minimi strumenti di scienza del costruire, MUP Editore, Parma, 2009.

Cerca sul sito

Il network Teknoring

Definizione

Generalità

Bibliografia

Allegati

www.Wikitecnica.com

Segui www.wikitecnica.com