Analisi strutturale

Analisi statica lineare agli elementi finiti: tensioni massime principali in una cupola poligonale.

Definizione-Etimologia

Dal greco analuo, sciogliere, analisi significa letteralmente decomposizione e quindi comprensione di un fenomeno attraverso la scomposizione nelle parti ed elementi che lo compongono. Riferita alle strutture, rappresenta il momento fondamentale di attribuzione e riconoscimento delle caratteristiche, permettendone la soluzione attraverso le leggi che ne governano il comportamento.
Con analisi strutturale, spesso sinonimo di calcolo strutturale, si indicano diversi strumenti e tecniche sviluppate nei secoli per interpretare e risolvere i problemi di meccanica delle strutture.

Scopi e strumenti

Scopo principale delle operazioni comprese nell’analisi strutturale è determinare, all’interno della struttura in esame o in una sua porzione, la distribuzione delle forze interne, dei momenti, delle tensioni, delle deformazioni e degli spostamenti.
L’analisi può essere condotta sull’intera struttura o separatamente sui singoli elementi costituenti, nel caso in cui la distribuzione degli sforzi su questi non sia omogenea, e gli strumenti utilizzati per eseguirla possono essere diversi in relazione alle differenti condizioni geometriche e di sforzo. Ogni metodo di calcolo adottato è legato a un modello strutturale che, oltre a essere risolubile, deve rappresentare in modo realistico il comportamento della struttura in esame.

Metodologie applicative

La fase di studio preliminare a ogni approccio analitico, indipendentemente dal modello interpretativo scelto, è rappresentata dalla semplificazione della geometria della struttura e dalla simulazione del comportamento dei materiali che la compongono.
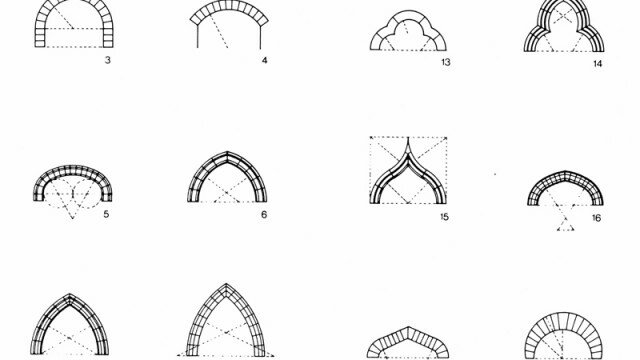
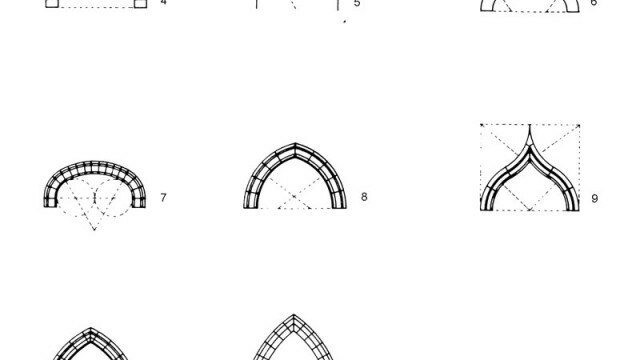
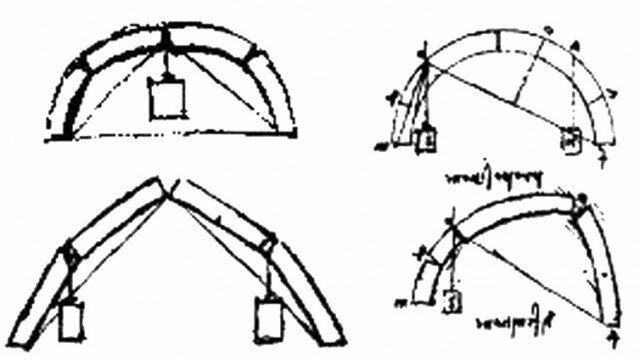
Per l’interpretazione del comportamento delle strutture antiche è spesso sufficiente la statica dei corpi rigidi, che, approssimando i materiali di deformabilità molto ridotta a infinitamente rigidi (quindi indeformabili), permette di risolvere la questione della stabilità riducendola all’equilibrio, e dunque al bilancio delle forze che agiscono sul corpo stesso. L’equilibrio della struttura si ricava dalle leggi fondamentali della statica (equazioni cardinali), configurandosi come quella particolare condizione in cui risultante e momento risultante siano uguali a zero. La riduzione del problema della stabilità alla questione dell’equilibrio è valida finché non ci si avvicini a valori caratteristici di rottura del materiale stesso (nelle strutture antiche, i materiali lavorano sempre a un livello di sollecitazione molto inferiore ai propri limiti di rottura), fornendo una buona stima delle quantità strutturali in gioco e rappresentando una prima analisi strutturale per strutture labili, in grado di garantire il proprio equilibrio solo per date condizioni di carico indipendentemente dal valore della resistenza dei materiali costituenti.

Sistemi statici ed elastici

La differenza tra i sistemi statici semplici in muratura, che restano in equilibrio “per tutti i valori di S [azione esterna] per i quali la risultante R [è] interna alla sezione d’appoggio”, e i primi sistemi elastici, che “riman[gono] in equilibrio anche per valori di S per i quali la risultante S sia completamente esterna alla sezione d’incastro”, è evidenziata da G.B. Milani nel suo trattato e sancisce l’evoluzione dell’analisi strutturale, che per questi ultimi deve considerare sia la resistenza dei materiali sia la distribuzione degli sforzi al loro interno.
Quando le forze sollecitanti la struttura sono considerate costanti nel tempo in ogni configurazione di carico, l’analisi strutturale è di tipo statico, mentre si dice dinamica quando si considerano forze variabili per intensità nel tempo (forze sismiche), simulando l’evoluzione della struttura, istante per istante, in ogni configurazione temporale e spaziale (edilizia antisismica).
Per la maggior parte dei dimensionamenti strutturali si possono utilizzare, almeno nella prima fase di validazione, calcoli di tipo statico, considerando la struttura in condizioni di equilibrio stazionario tra carichi esterni (forze, pressioni, campi non uniformi di accelerazione, temperature) e stato deformativo.

Analisi statica lineare

L’analisi di tipo statico lineare, secondo il metodo agli elementi finiti, è la più semplice che si possa condurre su una struttura, con l’ipotesi di piccoli spostamenti che consentono di scrivere le equazioni di equilibrio rispetto alla configurazione indeformata. Dato un corpo o un insieme di corpi, variamente vincolati, soggetti a un insieme di azioni applicate quasi staticamente, e realizzati con materiali che soddisfino la teoria dell’elasticità lineare, nell’ipotesi di piccoli spostamenti, l’analisi statica lineare permette di stabilire se la struttura esaminata sia o meno in grado di sopportare gli spostamenti, gli sforzi e le deformazioni conseguenti all’applicazione di queste azioni.

Metodo agli elementi finiti

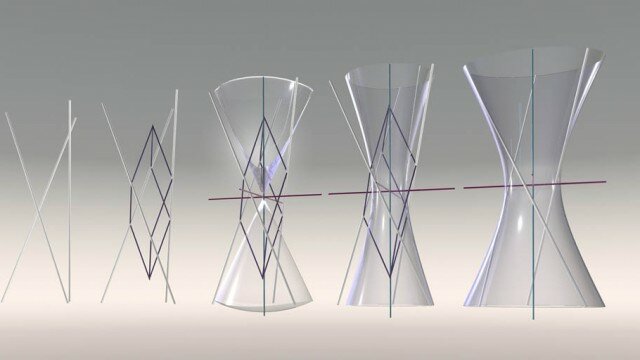
Il metodo agli elementi finiti (FEM) consiste nel suddividere la struttura in elementi più semplici (elementi finiti), i cui spostamenti, sforzi e deformazioni sono descrivibili tramite regole semplificate che richiedono la conoscenza degli spostamenti di pochi punti (nodi) dell’elemento stesso. Imposto l’equilibrio per questi punti, considerando forze e reazioni, l’intera struttura si riduce quindi a un sistema di equazioni che ha come termine noto il vettore delle azioni applicate e come incognita l’insieme degli spostamenti dei nodi, attraverso una costante di proporzionalità, detta matrice di rigidezza globale della struttura.
Scelto il tipo di analisi, si deve decidere quale modello matematico utilizzare, quale sia il tipo di elemento finito più adatto e come suddividere la struttura in elementi finiti (meshing), oltre che definire le caratteristiche geometriche e dei materiali, con la conseguente attribuzione dei vincoli e dei carichi per ogni condizione esaminata. Considerando il problema nell’ambito della teoria dell’elasticità, il sistema è risolvibile in forma chiusa (equazioni di Navier): noti gli spostamenti di tutti i nodi, la struttura è risolta, conoscendone spostamenti e deformazioni in ogni punto, sforzi e reazioni vincolari. Nel caso di geometrie complesse o irregolari e in particolari condizioni al contorno, la simulazione può richiedere un raffittimento della mesh in alcune zone della struttura.

Altri modelli di analisi

L’analisi statica non lineare consiste nella valutazione del comportamento sismico della struttura e della capacità di spostamento allo stato limite ultimo, da confrontarsi con lo spostamento in termini spettrali.
La maggior parte delle strutture reali è soggetta a vibrazioni e in queste condizioni un sistema può essere simulato a partire dal calcolo delle frequenze proprie e dei modi propri di vibrare, tramite simulazioni di dinamica strutturale come FRF (risposta in frequenza), analisi shock e random. L’analisi preliminare è la ricerca delle risonanze (analisi modale), che devono essere diverse dalle frequenze portanti delle eccitazioni periodiche che agiscono su un sistema o su un suo componente. L’analisi agli elementi finiti permette di individuare le frequenze di risonanza e le forme modali a esse associate e quindi di decidere come intervenire a livello progettuale per modificare le frequenze proprie del sistema stesso.

Bibliografia

Beer F.P., Johnston E.R., Vector Mechanics for Engineers, Singapore, 1990; Giuffré A., La meccanica nell’architettura, Roma, 1986; Milani G.B., L’ossatura murale, Torino, 1901.