Definizione

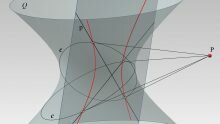
Dal punto di vista geometrico la sezione aurea “φ” indica la divisione (sezione) di un segmento in due parti, la maggiore delle quali (aurea) risulti media proporzionale fra l’intero segmento e la parte rimanente.

Cenni storici

Si riscontra nel pentagramma e nel pentagono, prediletti da Pitagora (VI-V secolo a.C.) e dai Pitagorici, nonché nel dodecaedro e nell’icosaedro, due fra i cinque poliedri regolari associati da Platone (V-IV secolo a.C.) alle strutture dell’universo.
Per altra via, tra il 1974 e il 1976 Roger Penrose e Robert Ammann sviluppano un modello di tassellazione dello spazio in simmetria icosaedrica perfettamente coincidente con l’organizzazione geometrica degli atomi dei “quasi-cristalli”, scoperta quasi dieci anni più tardi.
Coeva è la constatazione che la sezione aurea interviene anche nella geometria dei frattali, definendo il fattore di riduzione oltre cui le ramificazioni si intersecano.
Fra le più note configurazioni basate su questo rapporto è la spirale logaritmica, inscritta in un tracciato di quadrati e rettangoli aurei, curva dalle importanti analogie formali col profilo di accrescimento di alcune conchiglie, con la traiettoria di taluni volatili, e perfino con la tipica configurazione delle galassie.
Dal punto di vista algebrico le corrisponde il numero aureo “φ”, valore fisso “irrazionale” pari a 0.61803… con infinite cifre decimali prive di sequenze ripetute, nella pratica sempre approssimato.
Esso deriva dalla serie numerica 1,1,2,3,5,8,13, (…) di Leonardo Fibonacci (1180-1250) in cui ogni numero è dato dalla somma dei due precedenti, dove φ è precisamente il valore cui tende il rapporto fra due termini successivi (ad esempio, 13/8=1,625000, 987/610=1,618033, ecc.).
Il valore aureo sembra inoltre ben descrivere eventi artificiali e ricorrenze statistiche, incluse le fluttuazioni del mercato.
Interessanti riscontri si trovano anche nella produzione artistica visuale, plastica, musicale e letteraria.
Con riferimento all’architettura moderna Le Corbusier (1887-1965) è riconosciuto sostenitore dei contenuti estetici connessi alla relazione fra valori numerici e rapporti spaziali fondati sulla serie di Fibonacci. Nell’intento di ricondurre ogni configurazione a opportune combinazioni del rapporto aureo egli elabora, nella teoria del Modulor, due scale di numeri aurei basate su misure umane. Assumendo come dato “sorgente” l’altezza al plesso solare di un uomo di statura media che definisce il lato di un primo quadrato, mediante due semplici costruzioni, basate sul rapporto aureo e sui relativi legami col triangolo rettangolo e gli ulteriori due quadrati risultanti, rovesciando infine l’intera figura, nell’insieme un ampio rettangolo egli ritrova, scandite da trasversali sui lati lunghi: per un verso l’altezza del soggetto e l’altezza della mano del soggetto con braccio alzato come termini di una prima progressione di Fibonacci definita Serie Rossa; per altro verso, dall’altezza della mano con braccio alzato, ritrova più in basso l’altezza dell’altra mano con braccio lungo il busto quale termine di una seconda progressione di Fibonacci definita Serie Blu. Intesa come proporzione universale, in alcuni manifesti la rappresentazione degli intervalli aurei esorbita dal grande rettangolo contenente il profilo umano, convergendo in basso su valori di minuto dettaglio, e divergendo in alto su valori di scala ambientale. In coerenza con la dichiarata validità del metodo descritto, Le Corbusier suggerisce che il Modulor venga inteso non solo come principio ordinatore dello spazio ma anche della visione fisiologica, evidenziandosi pure nella progressione degli scorci apparenti la “scala variabile armonica delle possibilità percettive”.

Bibliografia

Herz-Fischler R., A Mathematical History of the Golden Number, Dover Publication, Mineola, NY, 1998;
Le Corbusier, Il Modulor + Modulor 2, FLC, Parigi, 2004; Livio M., La sezione aurea. Storia di un numero e di un mistero che dura da tremila anni, Rizzoli, Milano, 2003.

Sezione aurea curti-mario

www.Wikitecnica.com