Definizione – Etimologia

Isometria, dal greco isometrìa (eguaglianza di misura) è una trasformazione geometrica che conserva le lunghezze. Questa trasformazione può operare nel piano come nello spazio, nella geometria euclidea come in quelle non-euclidee.

Proprietà

Nel piano sussiste il seguente teorema fondamentale:

Tra due triangoli congruenti qualsiasi intercede una sola isometria.

Nello spazio, il medesimo teorema diventa:

Tra due tetraedri congruenti qualsiasi intercede una sola isometria.

Una isometria si dice diretta se conserva l’ordine degli elementi, inversa se lo inverte. La composizione di due o più isometrie fornisce ancora una isometria.

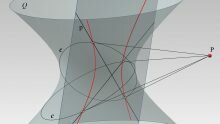
Esempi (fig. a)

Le isometrie che interessano il progetto di architettura sono: la traslazione, la rotazione, la simmetria centrale, la riflessione, la glisso riflessione.

Traslazione
Dati, nel piano o nello spazio, una figura f, una direzione orientata d, una lunghezza s, la traslazione f’ della figura f si ottiene costruendo, per ogni punto P di f, un segmento PP’ di lunghezza s, nella medesima direzione orientata d. L’insieme dei punti P’ costituisce la figura f’. La traslazione è una isometria diretta.
La sequenza di finestre aperte sulla facciata di un edificio a intervalli eguali, è un possibile esempio di traslazione nel piano. La sequenza di volumi identici e posti a intervalli eguali su un dato allineamento è un possibile esempio di traslazione nello spazio.

Rotazione (fig. b)
Nel piano, dati una figura f, un centro fisso O e un angolo orientato α, la rotazione f’ della figura si ottiene costruendo, per ogni punto P di f, un arco PP’ di centro O e ampiezza α. L’insieme dei punti P’ costituisce la figura f’.
Nello spazio, dati una figura f, un asse a e un angolo orientato α, la rotazione f’ della figura si ottiene costruendo, per ogni punto P di f, un piano π perpendicolare ad a, e, su questo, la rotazione P’ di P come sopra definita, essendo il centro di tale rotazione il punto O comune all’asse a e al piano π. La rotazione è una isometria diretta.
Gli edifici a pianta centrale presentano molti possibili esempi di questa isometria nel piano e nello spazio.

Simmetria centrale (fig. c)
Dati, nel piano o nello spazio, una figura f e un punto fisso O, detto centro di simmetria, la simmetrica f’ della figura f si ottiene costruendo, per ogni punto P della figura f il segmento PP’ tale che O ne sia il punto medio. L’insieme dei punti P’ costituisce la figura f’. La simmetria centrale nel piano è una isometria diretta, perché non inverte la successione degli elementi, mentre nello spazio è una isometria inversa.
Una simmetria centrale, rigorosamente applicata ad un edificio o ad una sua parte, produrrebbe, nella simmetrica f’, l’inversione delle parti più alte con quelle più basse.

Riflessione (fig. d)
Nel piano, dati una figura f e un asse di simmetria s, la figura f’ simmetrica di f si ottiene costruendo, per ogni punto P di f, il segmento PP’ perpendicolare all’asse s e tale che s lo tagli nel punto medio M. L’insieme dei punti P’ costituisce la figura f’. La riflessione nel piano si dice anche simmetria assiale.
Nello spazio, dati una figura f e un piano di simmetria σ, la figura f’ simmetrica di f si ottiene costruendo, per ogni punto P di f, il segmento PP’, perpendicolare al piano σ, e tale che σ lo tagli nel punto medio M. L’insieme dei punti P’ costituisce la figura f’.
La riflessione è una simmetria inversa.
La riflessione è senz’altro la isometria più facilmente osservabile in architettura: quasi tutti gli edifici storici, infatti, presentano questo tipo di simmetria, almeno nelle intenzioni di progetto. Il movimento moderno, invece, ha fatto della rottura di questo equilibrio uno dei suoi caratteri distintivi.

Glisso riflessione (fig. e)
La glisso riflessione è il prodotto di una riflessione e di una traslazione. Le orme di un uomo che cammina sulla sabbia sono legate da una glisso riflessione. La glisso riflessione è una isometria inversa. Corpi di fabbrica serviti, dalle due parti, da un percorso di distribuzione presentano questo tipo di isometria.

Bibliografia

Coxeter H., Introduction to Geometry, second edition, John Wiley & Sons, Inc., Hoboken, NJ, 1989; Weyl H., La simmetria, Feltrinelli, Milano, 1981.

Copyright © - Riproduzione riservata