Definizione – Etimologia – Uso
Il termine deriva dal latino superficies, composto di super e facies, quindi la “faccia che sta sopra”.
Superficie indica intuitivamente la parte esterna di un corpo, per Euclide “ciò che ha solo lunghezza e larghezza”, estensione bidimensionale del concetto di contorno, contrazione del concetto di solido astratto al suo confine ideale privo di spessore. Si usa con accezioni differenti come sinonimo di facciata, rivestimento, pelle, forma e anche area, quest’ultima affinità impropria nonostante faccia parte del linguaggio comune (ad esempio la superficie di un appartamento).
In ambito architettonico il termine è declinato in diverse forme: si definisce superficie topografica la costruzione discretizzata che sostituisce la superficie del terreno; la superficie agraria la proiezione del terreno su un piano orizzontale; il diritto di superficie l’edificare e mantenere al di sopra del suolo altrui una costruzione della quale si acquista una proprietà.
La superficie, oltre ad essere fisicamente l’oggetto materico dove sono tracciati i segni, è l’elemento bidimensionale destinato ad accogliere il contenuto dell’opera con la quale entra in relazione, campo di esistenza dell’atto figurativo magistralmente analizzato da Wassily Kandinsky nel celebre Punkt und Linie zu Fläche (traducibile come Punto e linea in relazione alla superficie).
Architettura
Il concetto di superficie in architettura si relaziona all’esterno della forma, da intendersi sia come ultimo strato di materia, sia come risultato formale che delimita spazio architettonico. Tali significati possono essere letti nelle loro linearità storica, nell’antica scissione fra facciata e pianta degli edifici storici ripresa fattivamente nella poetica moderna dei prospetti liberi, che si interfaccia alla contestuale attenzione al dettaglio frutto del Minimalismo. L’architettura contemporanea, infrangendo le limitazione del Moderno, si è sviluppata potenziando l’autonomia espressiva e decorativa della superficie, tema supportato anche dalle esigenze di prestazioni e efficienza energetiche sempre più affidate al rivestimento esterno. L’indipendenza della forma dalla struttura ha sconnesso definitivamente le superfici che diventano schermi anche morfologicamente complessi.
Geometria e rappresentazione
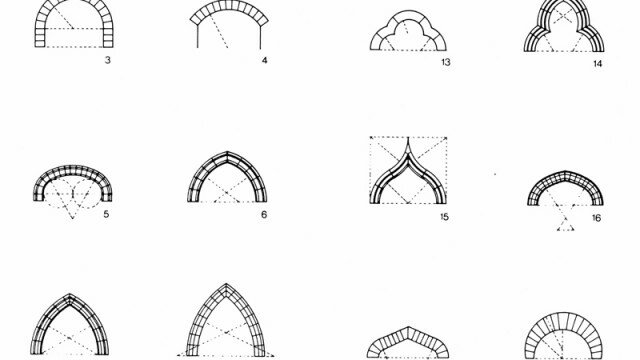
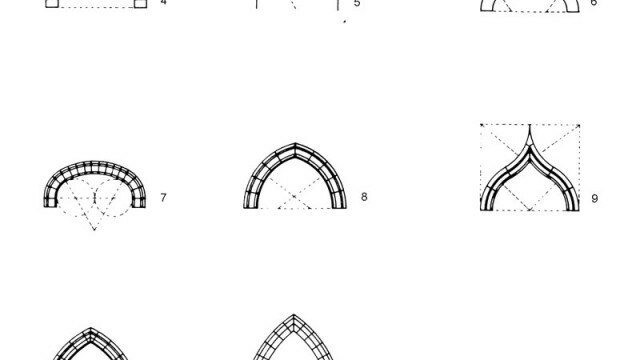
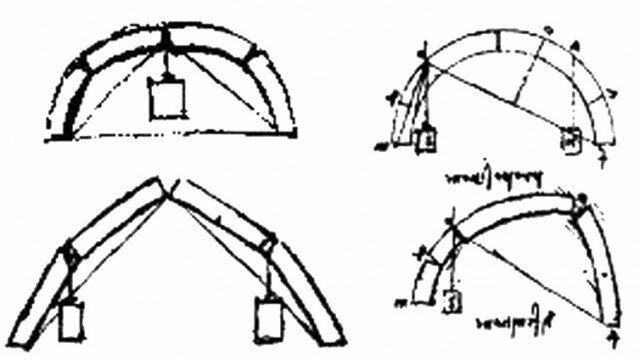
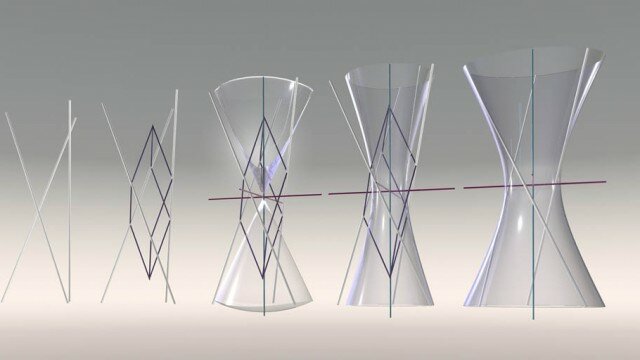
La superficie può essere definita come un luogo di punti che soddisfa una determinata equazione in tre variabili z=f(x, y). Per ciò che concerne il disegno dell’architettura, le proprietà delle superfici sono studiate dalla geometria descrittiva che ne analizza le caratteristiche in funzione del tipo. Diviene quindi centrale la classificazione delle superfici, il criterio interpretativo per costruire o leggere la forma ideata o rilevata. Esistono diversi modi per definire e classificare una superficie (analitico, algebrico, differenziale, topologico …), in architettura si predilige la classificazione come “luogo geometrico”, insieme di punti nello spazio che godono tutti della stessa proprietà, principio che ha acquisito un suo predominio gnoseologico per l’intrinseca congruità costruttiva. La costruzione della superficie è interpretata attraverso il movimento di “generatrici”, le linee che descrivono un contorno caratteristico, lungo le “direttrici”, le linee che guidano il moto ideale. Secondo tale logica, si possono definire in funzione della complessità del movimento superfici di traslazione (una generatrice qualsiasi che si sposta ponendo una direttrice lineare come binario), superfici di rivoluzione (una generatrice qualsiasi che ruota con movimento rigido ponendo una direttrice lineare come asse), superfici rigate (una generatrice retta che si muove lungo una direttrice lineare con moto rototraslatorio), superfici di rototraslazione (una qualsiasi generatrice che si muove avendo una direttrice contestualmente come asse e come binario). Tale classificazione, utile alla costruzione del modello e alla rappresentazione, soprattutto grazie alla rivoluzione infografica del disegno si è arricchita di una generalizzazione definita dalle superfici di interpolazione che pongono la possibilità di una contestuale trasformazione delle generatrici e delle direttrici. Con la terminologia che deriva dalla pratica del disegno digitale, questa superclasse può essere discretizzata in superfici loft (interpolazione della generatrice che si trasforma lungo una direttrice implicitamente data), superfici monodirezionali (interpolazione del movimento della generatrice lungo una direttrice generica data), superfici bidirezionali (interpolazione della generatrice trasformata lungo due direttrici generiche date), superfici di punti (interpolazione di punti dati nello spazio), superfici di bordo (interpolazione degli elementi contigui di contorno), superfici proporzionali (interpolazione una rete di linee senza differenza fra generatrici e direttrici).
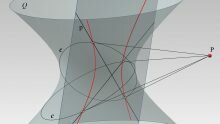
La superficie può essere piana o curva, chiusa o aperta, virtualmente illimitata ma nell’uso pratico segnata da curve di confine (superficie trimmed), con i modelli genericamente composti da porzioni di superfici (patches). Fra gli elementi contigui, si può stabilire la continuità di posizione (G0) nel caso di un bordo o di una porzione in comune, la continuità di tangenza (G1) nel caso della condivisione dello stesso piano tangente, la continuità in curvatura (G2) nel caso dell’uguaglianza del cerchio osculatore. In ogni punto P della superficie è possibile misurare la curvatura come il prodotto delle due curvature principali, la massima (K1) e la minima (K2), ottenute dall’intersezione della superficie con un piano passante per la normale in P. Alle curvature principali è assegnato un valore positivo o negativo a seconda della posizione del cerchio osculatore rispetto la direzione della normale e si definisce la curvatura gaussiana K=(K1*K1), caratteristica che determina lo stato locale della forma in quanto se K≠0, la superficie localmente è a doppia curvatura, altrimenti è a singola curvatura. La curvatura gaussiana definisce anche la natura del punto analizzato: “elittico” se K>0, cioè quando le curvature sono entrambe o concave o convesse; “iperbolico” se K<0, cioè quando sono opposte; “parabolico” se K=0, quindi se sono entrambe pari a zero (piano) o se è nulla solamente una (punto parabolico).
Nel linguaggio del disegno digitale la rappresentazioni delle superfici, boundary representation (B-Rep), si distingue dalla constructive colid ceometry (CGS) perché permette la rappresentazione dei volumi per mezzo dei suoi limiti tipologici (facce, bordi e vertici) e geometrici (punti, linee e aree). La superficie può essere generata attraverso la “rappresentazione matematica” o la “rappresentazione numerica”: nella prima accezione si intende una rappresentazione con equazioni parametriche, generate da una curva di parametro u che si muove nello spazio seguendo una traiettoria con parametro v, che si trascrive in forma vettoriale P=P(u,v); la rappresentazione numerica di una superfici avviene attraverso un poliedro descritto da m poligoni genericamente di n lati posti a regolarizzare la frontiera dell’oggetto e in tal caso gli elementi caratteristici sono i vertici, i bordi e le facce del poliedro descritto, connessi solitamente attraverso simplessi bidimensionali (triangoli) in modo da definire un complesso simpliciale (aggregazione ordinata di simplessi).
Bibliografia
Balmond C., Informal, Berlin, 2002; Burroughs C., The Italian Renaissance Palace Façade, Cambridge, 2002; Leatherbarrow D., Mostafavi M., Surface Architecture, Boston, 2002; Kandinsky W., Punkt und Linie zu Fläche, München, 1926; Knaack U. et alii, Façades: principles of construction, Basilea, 2007;
Migliari R., Geometria descrittiva, Novara, 2009; Rolando A., Forma, Geometria, Struttura, Milano, 2008; Schumacher P., The autopoiesis of architecture: a new framework for architecture, London, 2011.

Ipotesi di classificazione tipologica delle superfici.
Copyright © - Riproduzione riservata